model.md

title: Implementing a Model in DuMuX

What is a DuMu^X model

What is a DuMu^X model

A DuMu^X model is an implementation of a discretized mathematical model, generally given by partial differential equations.

What is a DuMu^X model

Mathematical model (PDE):

There was an error rendering this math block. KaTeX parse error: {equation*} can be used only in display mode.

Discrete model, e.g. using finite volumes:

There was an error rendering this math block. KaTeX parse error: {equation*} can be used only in display mode.

What is a DuMu^X model

Discrete model, e.g. using finite volumes:

There was an error rendering this math block. KaTeX parse error: {equation*} can be used only in display mode.

• $S_h$
  : storage term
• $F_{B,\sigma}$
  : flux term over sub control volume face (scvf)
• $q$
  source term

Where to implement these terms in DuMu^X?

LocalResidual

LocalResidual

LocalResidual

Implements terms of a PDE in the functions

• computeStorage(...)
• computeFlux(...)
• computeSource(...)

Example: Diffusion equation

Mathematical model (PDE):

There was an error rendering this math block. KaTeX parse error: {equation} can be used only in display mode.

with

• $c$
  : concentration
• $D$
  : constant diffusion coefficient
• $\Omega$
  : spatial domain
• $T$
  : end time

Example: Diffusion equation

Discrete model using the Box discretization:

There was an error rendering this math block. KaTeX parse error: {equation} can be used only in display mode.

with

• $c_B^n$
  : concentration at time
  $t_n$
  and control volume
  $B$
• c^n_h
  : global discrete solution at time
  t_n
  , interpolated using basis functions
• \mathbf{n}
  : unit outer normal vector
• \sigma
  : sub control volume face (scvf)

Example: Diffusion equation

Discrete model using the Box discretization:

\begin{equation} \vert B \vert \frac{c_B^{n+1}-c_B^{n}}{\Delta t} - \sum_{\sigma \in \Sigma_{B}} \left[ D \nabla c_h^{n+1} \cdot \boldsymbol{n}_{B,\sigma} \vert \sigma \vert \right] = 0, \end{equation}

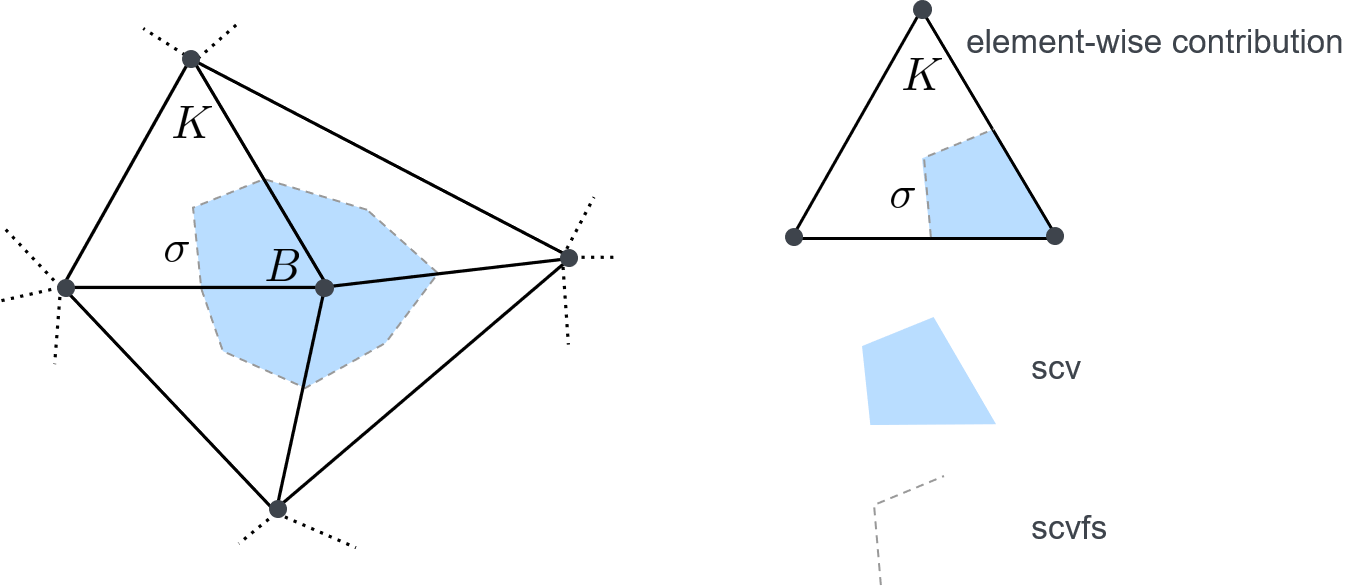
LocalResidual

The local residual of the diffusion model:

template<class TypeTag>
class DiffusionModelLocalResidual
: public GetPropType<TypeTag, Properties::BaseLocalResidual>
{
    ...
}

Inherits from the BaseLocalResidual, which is chosen depending on the discretization scheme, here Box scheme.

Storage term

NumEqVector computeStorage(const Problem& problem,
						   const SubControlVolume& scv,
						   const VolumeVariables& volVars) const
 {
    NumEqVector storage;
    storage[Indices::massBalanceEqIdx]
        = volVars.priVar(Indices::concentrationIdx);
    return storage;
 }

Flux term

\begin{equation} F_{B,\sigma} = -D \nabla c_h^{n+1} \cdot \boldsymbol{n}_{B,\sigma} \vert \sigma \vert \end{equation}

with

• c^n_h
  : global discrete solution at time
  t_n
  , interpolated using basis functions
• \mathbf{n}
  : unit outer normal vector
• \sigma
  : sub control volume face (scvf)

Flux term

NumEqVector computeFlux(const Problem& problem,
                        const Element& element,
                        const FVElementGeometry& fvGeometry,
                        const ElementVolumeVariables& elemVolVars,
                        const SubControlVolumeFace& scvf,
                        const ElementFluxVariablesCache& elemFluxVarsCache) const
{
    ...
}

Flux term

NumEqVector computeFlux(...) const
{
    // Compute ∇c
    const auto& fluxVarCache = elemFluxVarsCache[scvf];
    Dune::FieldVector<Scalar, dimWorld> gradConcentration(0.0);
    for (const auto& scv : scvs(fvGeometry))
    {
        const auto& volVars = elemVolVars[scv];
        gradConcentration.axpy(
            volVars.priVar(Indices::concentrationIdx),
            fluxVarCache.gradN(scv.indexInElement())
        );
    }
    ...
}

Flux term

NumEqVector computeFlux(...) const
{
    ...
    NumEqVector flux;

    // Compute the flux
    flux[Indices::massBalanceEqIdx] = -1.0*scvf.area()*vtmv(
        scvf.unitOuterNormal(),
        problem.diffusionCoefficient(),
        gradConcentration
    );

    return flux;
}

LocalResidual

A LocalResidual implements the discretized mathematical model.

For its implementation different model-specific properties have to be set

Model properties

Model type tag

The property tag is an empty struct with the respective name, e.g. DiffusionModel

namespace Dumux::Properties::TTag {
//! The diffusion model tag that we can specialize properties for
struct DiffusionModel {};
} // end namespace Dumux::Properties::TTag

Model properties

We can set nodel properties for the DiffusionModel type tag

All properties are defined within the namespace Dumux::Properties

namespace Dumux::Properties {
    //define all properties
} // end namespace Dumux::Properties

Defining model properties

The type of the local residual is the class DiffusionModelLocalResidual defined from earlier

template<class TypeTag>
struct LocalResidual<TypeTag, TTag::DiffusionModel>
{ using type = DiffusionModelLocalResidual<TypeTag>; };

Defining model properties

The model traits specify information about the model:

template<class TypeTag>
struct ModelTraits<TypeTag, TTag::DiffusionModel>
{
    struct type
    {
        struct Indices
        {
		    static constexpr int concentrationIdx = 0;
		    static constexpr int massBalanceEqIdx = 0;
        };
        static constexpr int numEq() { return 1; }
    };
};

Defining model properties

Further model specific properties can be set accordingly by using the model property tag, i.e. TTag::DiffusionModel

Exercise: Model

Exercise: Model

Implementation of a nonlinear diffusion model for denoising of an MRI image

Tasks

• Implement local residual
• Set model properties
• Use model in test case
• Customize volume variables